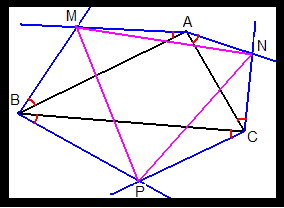
Let ABC be any triangle you draw.

From each vertex, draw two lines outside the triangle, each one at 30' (red arcs) with the sides that meet each other in the vertex.

These 6 lines cross, two by two, at 3 points, named M, N, and P.

Prove that, no matter what triangle ABC you draw initially, the triangle MNP is always equilateral.

(In reply to re: Napoleon's Theorem by pcbouhid)

I don't know of any purely geometric proof, but I have a trigonometric proof.

First, define some variables:
Let D be the measure of angle CAB
Let E be the measure of angle ABC
Let F be the measure of angle BCA
Let 2*d be the measure of BC
Let 2*e be the measure of AC
Let 2*f be the measure of AB

Applying the law of sines and law of cosines to triangle ABC yeilds:
cos D = (-d^2 + e^2 + f^2)/(2ef)
cos E = (d^2 - e^2 + f^2)/(2df)
cos F = (d^2 + e^2 - f^2)/(2de)
(sin F)/(2f) = (sin E)/(2e) = (sin D)/(2d)

Applying the law of cosines to triangles AMB, BPC, and CNP yields three equations using only the defined variables:
MP^2 = 3f^2 + 3d^2 - 6df*cos[E+60]
PN^2 = 3d^2 + 3e^2 - 6de*cos[F+60]
NM^2 = 3e^2 + 3f^2 - 6ef*cos[D+60]

The three expressions for the sides of MNP are symmetric, therefore proving any two are equal implies all three are equal.

Taking MP=PN yields:
f^2 - 2df*cos[E+60] = e^2 - 2de*cos[F+60]

Expanding the cosines using the cosine sum identity:
f^2 - df*cos[E] + sqrt[3]*df*sin[E] = e^2 - de*cos[F] + sqrt[3]*de*sin[F]

The two terms sqrt[3]*df*sin[E] and sqrt[3]*de*sin[F] are equal according to the sine equation above.  Cancelling those terms and substituting expressions for cos[E] and cos[F] yields:
f^2 - df*(d^2 - e^2 + f^2)/(2df) = e^2 - de*(d^2 + e^2 - f^2)/(2de)

Each side of the equation reduces to (e^2+f^2)/2, therefore MP does equal PN and by symmetry MNP is equilateral.

Posted by Brian Smith on 2008-10-21 03:07:30