The network represents a map of the edges and vertices of a
hypercube or more precisely, a tesseract when imposed within 2D space.
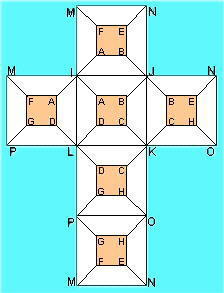 |
The orange squares represent the faces of the internal cell, a cube in 3D space, and is defined by vertices A to H. The larger bolder letters, I to P are the vertices of the outer cell/cube.
The diagonal lines are the edges which link the inner to the outer forming the faces that configure the cells which interface to the inner and outer cells.
Let each hypercell have a value which is the vertex sum of each of its enclosing faces (or three times the sum of its 8 vertices).
|
The vertices are to be numbered uniquely from 1 to 16, and for consistency of reference, let
A always be 1.
Find sets of values for A through P so that all the cells have the same value.
Note: while the on-line calculator may be useful, a spreadsheet should prove more valuable for those able to use one.
(In reply to
computer solution by Charlie)
The use of B < C < I < F to determine unique solutions without counting alternative rotations and reflections was based upon all the 1-D edges coming out of A leading to each of those vertices, so they would be interchangeable in defining the nature of the topology.
However, I noticed that while cell ADFGILMP is used in the calculator portion, and, based on that, in my computations, that the diagram shows cell ACFGILMP. There had been mention in the queue of a mix-up between C and D, and I think that mix-up is still present. I need to revise the computations based on B < D < I < F, as D, rather than C, should be adjacent to A.
The solutions presented are all valid, but probably my count is off as to how many solutions there are, as it may contain topologically equivalent solutions and may be missing others.
|
|
Posted by Charlie
on 2009-02-03 12:00:15 |




