Still smarting from his rather embarrassing loss, Harvey the Hare appealed to Aesop for a rematch against Tommy the Tortoise. After giving it much thought to make any such race as fair as possible, knowing that Harvey can run exactly 50 times as fast as Tommy, Aesop agreed to the new race but only under the following odd and seemingly unfair conditions:

1. This time, each would start/finish the race at the same point, but would run on separate (occasionally intersecting) courses of different lengths. Harvey's course consists of three straight legs, while Tommy's course runs along the external arcs of 3 tangent (non-overlapping) circles having radii greater than 5 and less than 10 feet.
2. The second leg of each course was 2 feet longer than the first leg, while the third leg for each was 2 feet longer than the second.
3. The "infield" areas enclosed by each course in (square) feet were both 4 times the total length of the respective course in feet.
4. But most surprisingly of all, Aesop insisted that Harvey got to run the shorter of the two courses!!!

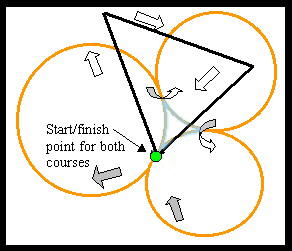
Note that the graphic is not to scale.
What were the lengths of Harvey and Tommy's respective race courses, and the area enclosed by each, in feet?

Bonus question!

Race day arrived, with throngs of story book characters arriving to cheer along their favourite runner (although Rip van Winkle did sleep through the whole thing, and Sneezy was laid up at home with a cold!)

Mother Goose as the Official Starter popped a balloon and the two were off! Not surprisingly, Harvey was away like a shot and in true fable form, given his superior speed, decided that a nap along the way would once again be in order. After snoozing for exactly 60 minutes, however, the roar of the crowd cheering Tommy along to the finish line woke Harvey up, but despite his best efforts, he lost the race yet again, this time by less than 30 seconds!

To one decimal place, what were Tommy and Harvey's running speeds in feet/minute?

(Hint: Since this is, after all, a fable, you can ignore any acceleration, topography, wind, "cornering" issues, etc. Just assume that when they run, both Tommy and Harvey run flat out at a constant speed.)

(In reply to re: Complete solution by brianjn)

well my understanding is that since in order to compute the arc lengths for the circular track you must know the angle of the arcs, and so in order to be able to solve for the arc lengths exactly you would have to be able to find the Cosine of the angles exactly and thus the angles must be an angle for which algebraic trig values are know.  For the radii I found I converted the angles of the arcs to degrees and it does not appear that they are any of the angles for which algebraic trig values are known so it would appear to me that numeric methods are neccesary for determining the measurements of the circular based track but if Rod is aware of a simple geometric method of solving for the radii then it is quite beyond me to be able to find it and I anticipate either him revealing it in his solution or someone else more talented than I in geometry to discover it.

As for the triangle track there may be a simple geometric approach but my geometry is weak enough that I will leave its discovery for someone else.  But it is possible that the simple solution that Rod refers to is in fact the Heron formula.

Posted by Daniel on 2009-03-27 05:24:08