Still smarting from his rather embarrassing loss, Harvey the Hare appealed to Aesop for a rematch against Tommy the Tortoise. After giving it much thought to make any such race as fair as possible, knowing that Harvey can run exactly 50 times as fast as Tommy, Aesop agreed to the new race but only under the following odd and seemingly unfair conditions:

1. This time, each would start/finish the race at the same point, but would run on separate (occasionally intersecting) courses of different lengths. Harvey's course consists of three straight legs, while Tommy's course runs along the external arcs of 3 tangent (non-overlapping) circles having radii greater than 5 and less than 10 feet.
2. The second leg of each course was 2 feet longer than the first leg, while the third leg for each was 2 feet longer than the second.
3. The "infield" areas enclosed by each course in (square) feet were both 4 times the total length of the respective course in feet.
4. But most surprisingly of all, Aesop insisted that Harvey got to run the shorter of the two courses!!!

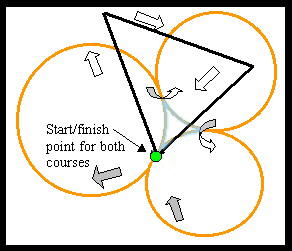
Note that the graphic is not to scale.
What were the lengths of Harvey and Tommy's respective race courses, and the area enclosed by each, in feet?

Bonus question!

Race day arrived, with throngs of story book characters arriving to cheer along their favourite runner (although Rip van Winkle did sleep through the whole thing, and Sneezy was laid up at home with a cold!)

Mother Goose as the Official Starter popped a balloon and the two were off! Not surprisingly, Harvey was away like a shot and in true fable form, given his superior speed, decided that a nap along the way would once again be in order. After snoozing for exactly 60 minutes, however, the roar of the crowd cheering Tommy along to the finish line woke Harvey up, but despite his best efforts, he lost the race yet again, this time by less than 30 seconds!

To one decimal place, what were Tommy and Harvey's running speeds in feet/minute?

(Hint: Since this is, after all, a fable, you can ignore any acceleration, topography, wind, "cornering" issues, etc. Just assume that when they run, both Tommy and Harvey run flat out at a constant speed.)

(In reply to re: Complete solution by Bractals)

Below is a list of the cell names and values in my spread sheet

r1 6.217946003
r2 6.546281207
r3 6.873462158
s1 13.41974337
s2 13.09140816
s3 12.76422721
t1 1.09115801
t2 1.046059997
t3 1.004374646
sm 19.63768937
art 74.12313304
ar1 21.09364059
ar2 22.41382172
ar3 23.72557997
arc 6.890090747
area 411.4051177
arc1 32.28374538
arc2 34.283695
arc3 36.28370531
goal 1 0.000534895
goal 2 5.0384E-05
goal 3 1.03178E-05
sq dev 2.88758E-07

and the equations used for each are

r1,r2,r3 are the radii being sought for and thus are the 3 cells that the solver changed to seek the final solution

s1,s2,s3 are the lengths of the sides of the triangle formed by joining the 3 circle centers and thus are

s1=r2+r3, s2=s1+s3, and s3=s1+s2

t1,t2,t3 are the angles across from sides s1,s2,s3 respectivly and were computed using the cosine law as follows

t1=acos((s2^2+s3^2-s1^2)/(2*s2*s3))

t2=acos((s1^2+s3^2-s2^2)/(2*s1*s3))

t3=acos((s1^2+s2^2-s3^2)/(2*s1*s2))

sm is the semi-perimeter of the triangle s1,s2,s3 and thus

sm=(s1+s2+s3)/2 and is used to compute area of traingle in next cell art (for ARea Triangle) and thus is

art=sqrt(sm*(sm-s1)*(sm-s2)*(sm-s3))

ar1,ar2,ar3 are the areas of the circle sectors made by angles t1,t2,t3 respectively and thus are

ar1=(t1/2)*r1^2, ar2=(t2/2)*r2^2, ar3=(t3/2)*r3^2

arc is the area of the central region inclosed by the "arc-triangle" in the middle of the diagram and thus is

arc=art-ar1-ar2-ar3

area is the total area inclosed by the track and is thus

area=arc+pi*(r1^2+r2^2+r3^2)

arc1,arc2,arc3 are the 3 arcs that form the 3 legs of the track on circles r1,r2,r3 respectively and thus are

arc1=(2*pi-t1)*r1, arc2=(2*pi-t2)*r2, arc3=(2*pi-t3)*r3

goal1, goal2, goal3 are the 3 goals which are being sought and these are that we want area to be equal to 4 times arc1+arc2+arc3 so I set goal1=abs(area-4*(arc1+arc2+arc3)), goal2 and goal3 are concerning our need for arc2-arc1=2 and arc3-arc2=2 and so I set goal2=abs(arc2-arc1-2) and goal3=abs(arc3-arc2-2) and so we want each of goal1,goal2, and goal3 to be as close as possible to 0 and thus I used st dev=goal1^2+goal2^2+goal3^2 to summary this overall goal.

So finally I set the solver to modify cells r1,r2,r3 with the goal of getting cell st dev as close to 0 as possible and the further restriction that r1 is between 5 and 10 and r2 between r1 and 10 and r3 between r2 and 10.  And it was able to find the solution given in my previous post.  If anybody would like they can email me and I would be more than happy to email them a copy of the spreadsheet used.

*I cleaned up the table in the first part so it should now be readable, also I am going to paste below here the actual excel equations used.*

on here the first row starts with r1 being in cell A1 and 5 in B1 and so on down the columns

Col A  Col B
r1  5
r2  5
r3  5
s1  =b2+b3
s2  =b1+b3
s3  =b1+b2
t1  =ACOS((B5^2+B6^2-B4^2)/(2*B5*B6))
t2  =ACOS((B4^2+B6^2-B5^2)/(2*B4*B6))
t3  =ACOS((B4^2+B5^2-B6^2)/(2*B4*B5))
sm  =(B4+B5+B6)/2
art  =SQRT(B10*(B10-B4)*(B10-B5)*(B10-B6))
ar1  =(B7/2)*B1^2
ar2  =(B8/2)*B2^2
ar3  =(B9/2)*B3^2
arc  =B11-B12-B13-B14
area  =B15+PI()*(B1^2+B2^2+B3^2)
arc1  =(2*PI()-B7)*B1
arc2  =(2*PI()-B8)*B2
arc3  =(2*PI()-B9)*B3
goal 1  =ABS(B16-4*(B17+B18+B19))
goal 2  =ABS(B18-B17-2)
goal 3  =ABS(B19-B18-2)
sq dev  B20^2+B21^2+B22^2

Edited on March 27, 2009, 10:10 pm

Posted by Daniel on 2009-03-27 16:17:56