For the arbitrary triangle ABC in the figure below, prove that:
1) The yellow area is three times the cyan area.
2) The magenta area is five times the red area.
Note: The yellow and cyan areas are squares.
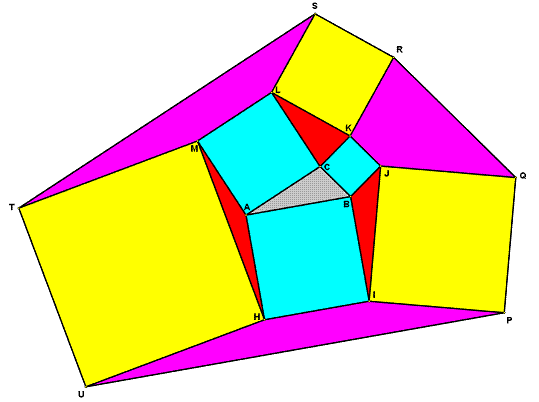
let a=AC, b=BC, and c=AB
also let angles CBA, CAB, and ACB be x,y,z respectively
and let p=HM, q=LK, and r=JI
now we have the cyan area easily as a^2+b^2+c^2
to find p:
we can get angle MAH as 2π-π-π-y=π-y
and then from the law of cosines we have
p^2=a^2+b^2-2*a*b*cos(π-y)=a^2+b^2+2ab*cos(y)
we also have
b^2=a^2+c^2-2ab*cos(y) and thus
cos(y)=(a^2+c^2-b^2)/(2ab)
and substituting we get
p^2=2a^2+2c^2-b^2
and using similar methods we get
q^2=2a^2+2b^2-c^2
and
r^2=2b^2+2c^2-a^2
and thus the total yellow area is simply
3(a^2+b^2+c^2)
which is indeed 3 times the cyan area
now for the fun part, the magenta/red areas
|
|
Posted by Daniel
on 2009-06-17 13:07:25 |



