Construct the set of all points which are at distance r from some point on the square.

Find the area of this set.

Note: A square is composed of 4 line segments, not the interior. For some values of r the set will have a hole in it.

Example of the construction:

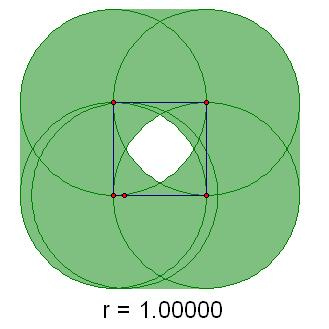
If it were not for the hole, the shape would consist of the original square surrounded by 4 1xr rectangles and 4 quarter-circles of radius r. That would have an area of 1 + 4r + pi*r^2.

There is no hole when 1/2 <= r <= sqrt(2) / 2, and so in this range:

A = 1 + 4*r + pi*r^2

When r <= 1/2, the hole is a square (1-2*r)x(1-2*r), so in this range:

A = 1 + 4*r + pi*r^2 - (1 - 2*r)^2
  = 8*r + (pi - 4)*r^2
 
But when r >= sqrt(2)/2, the hole in the middle is complicated.

That hole is a square tilted 45° to the original square, surrounded by segments of circles centered upon the corners of the original square.

The apex of the tilted square has a distance from the center of the opposite side of the original square that is equal to what we will call 1/2 + s, where s is half the diagonal length of this smaller square. The value of s can be found from the Pythagorean relation:

r^2 = (1/2 + s)^2 + (1/2)^2

As s needs to be positive, the quadratic formula gives:

s = (sqrt(1 + 4*(r^2 - 1/2)) - 1) / 2

The area of the tilted square making up most of the central hole is then 2 * s^2, or

(sqrt(1 + 4*(r^2 - 1/2)) - 1)^2 / 2

A circular segment has area r^2 * (theta - sin theta) / 2, when theta is the radian measure of the segment's chord angle at the center of curvature.

Theta = 2*arcsin (s * sqrt(2) / (2*r))

The hole consists of the area of the tilted square plus 4 times the area of this segment, as there are four such segments.

So the total area of the hole is:

(sqrt(1 + 4*(r^2 - 1/2)) - 1)^2 / 2 + 2 * r^2 * (theta - sin theta)

I'd hate to make all the substitutions necessary for the formula to be expressed solely in terms of r.