Construct the set of all points which are at distance r from some point on the square.

Find the area of this set.

Note: A square is composed of 4 line segments, not the interior. For some values of r the set will have a hole in it.

Example of the construction:

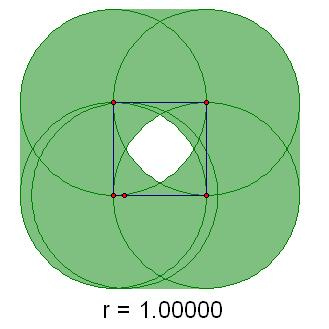
The area of the set is pi*r^2+4*r+1 minus the
area of the center hole.

For r < 1/2, 

   Area of center hole = (1-2*r)^2

For 1/2 <= r <= sqrt(2)/2,

   No center hole

For sqrt(2)/2 < r,

   Area of center hole 

          -- sqrt(r^2 - 1/4)
          |
          |
     =  4 | [sqrt(r^2 - x^2) - 1/2] dx
          |
          |
         -- 1/2  

     = 2*r^2*[arctan(t)-arctan(1/t)] - t + 1

       where t = 2*sqrt(r^2 - 1/4) and

       arctan returns radians.