Construct the set of all points which are at distance r from some point on the square.

Find the area of this set.

Note: A square is composed of 4 line segments, not the interior. For some values of r the set will have a hole in it.

Example of the construction:

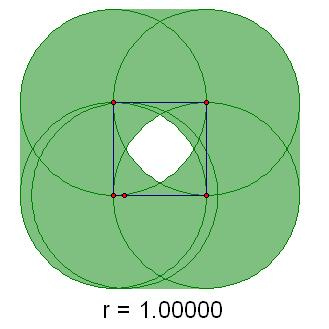
Bractals' and my formulas for the area of the center hole for r >= sqrt(2)/2 agree numerically:

DECLARE FUNCTION arcsin# (x#)
DEFDBL A-Z

FOR r = .8 TO 1.2 STEP .1
  s = (SQR(1 + 4 * (r ^ 2 - 1 / 2)) - 1) / 2
  theta = 2 * arcsin(s * SQR(2) / (2 * r))
  a = (SQR(1 + 4 * (r ^ 2 - 1 / 2)) - 1) ^ 2 / 2 + 2 * r ^ 2 * (theta - SIN(theta))
  PRINT USING "##.## ##.########"; r; a;

  t = 2 * SQR(r ^ 2 - 1 / 4)
  a = 2 * r ^ 2 * (ATN(t) - ATN(1 / t)) - t + 1
  PRINT USING "     ##.########"; a
NEXT

FUNCTION arcsin (x)
 d = SQR(1 - x * x)
 arcsin = ATN(x / d)
END FUNCTION

 r    Area(Charlie)   Area(Bractals)
0.80  0.03328298      0.03328298
0.90  0.13956677      0.13956677
1.00  0.31514677      0.31514677
1.10  0.55792407      0.55792407
1.20  0.86664457      0.86664457