You can navigate the grid below from the top-left yellow circle to the bottom-right yellow square by making only orthogonal (not diagonal) moves, going from one position to the next only if the shape and/or the color of the shape in the entered cell is the same as that of the cell you are leaving.
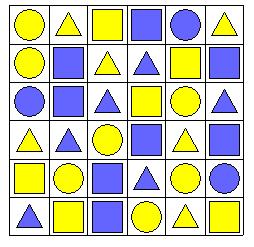
-
What path has the minimum number of moves without going through the same cell twice?
-
What path has the maximum number of moves without going through the same cell twice?
I found the simplest approach to be to draw a simple graph using the midpoints of each square. Connect orthogonally adjacent squares if the conditions are met (same color or same shape), otherwise no connection. From this diagram it it obvious that only a few paths exist from upper left to lower right.
It only takes a minute or so of inspection to note that the shortest path is 18 viz (1,1)(2,1)(3,1)(3,2)(4,2)(4,1)(5,1)(5,2)(6,2)(6,3)(5,3)(5,4)(4,4)(3,4)(3,5)(4,5)(5,5)(6,5)(6,6).
For the longest path, using the same graph, remove the segments which have only a single segment (both 1,1 and 6,6 have two; any square with only a single segment entering is excluded because to enter and leave would require visiting the same square twice.
There is a cut point from 1,1 to 3,2: the longest way to reach 3,2 is [(1,1)(1,2)(1,3)(1,4)(2,4)(2,3)(3,3)(3,2)] entering 7.
From 3,2 to 3,5 there is only a single path [(3,2)(4,2)(4,1)(5,1)(5,2)(6,2)(6,3)(5,3)(5,4)(4,4)(3,4)(3,5)] entering 11 (this is part of the shortest path).
From 3,5 to 5,5 there are only two paths, the longer of which is [(3,5)(2,5),(2,6),(3,6)(4,6)(5,6)(5,5)] entering 6.
From 5,5 to 6,6 you may choose either [(5,5)(5,6)(6,6)] or [(5,5)(6,5)(6,6)] entering 2.
Hence the longest path meeting the qualifications is 26. This all seems straightforward: working with the graph seemed much simpler for visualization than working repeatedly with the shapes and colors per se. Unless I was careless with my graph, this seems quickly to solve both tasks. No computer needed!



