A few of things occur to me off the top pf my head. I'm not sure how many will be useful in solving the problem.
Andle DEA = Angle DAE
Angle BDE = 2 * Angle BAC
Law of Sines:
sin (BAC)/(BC) = sin (ABC)/(AC) = sin (ACB)/(AC)
and
sin(DAE)/(DE) = sin(ADE)/(AE) = sin(AED)/(AE)
Law of Cosines:
(BC)^2= (AB)^2 + (AC)^2 -2 (AB)(AC)(cos[BAC])
(AC)^2= (AB)^2 + (BC)^2 -2 (AB)(BC)(cos[ABC])
(BA)^2= (CB)^2 + (AC)^2 -2 (CB)(AC)(cos[BCA])
and
(DE)^2= (AD)^2 + (AE)^2 -2 (AD)(AE)(cos[DAE])
(AD)^2= (AE)^2 + (DE)^2 -2 (AE)(DE)(cos[AED])
(AE)^2= (AD)^2 + (DE)^2 -2 (AD)(DE)(cos[ADE])
Since we are looking for Angle BAC or Angle DAE, which is the same angle) then solving for cos (BAC) seems to be the most promising route, especially when we can substitute using:
(AE) + (EC) = AE and
(AD) = (DE) = (EC)
|
|
Posted by TomM
on 2002-06-18 02:20:23 |
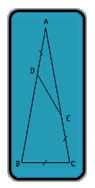 Given that:
Given that:


