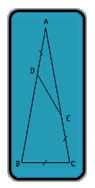
First deal with the degenerate cases:

If AD = DE = EC = BC = 0, then B and C are the same point and angle A = 0; If AE = DB = 0 then AB coincides with AD and AC coincides with EC and DE coincides with BC and you get Friedlinguini's equilateral triangle.

In the non-trivial case use the Law of Cosines on triangle DAE. Since no scale was given for the lengths of the line segments, set it in such a way as to reduce the algebra involved: AD = 1; AE = x; AC = (x + 1)

1^2 = 1^2 + x^2 - 2x(cosA)
1 = 1 + x^2 -2x(cosA)
2x(cosA) = x^2
cosA = x/2

Then use the Law of Cosines on triangle BAC

1^2 = (x + 1)^2 + (x + 1)^2 - 2(x + 1)(x + 1)cosA
1 = 2[(x + 1)^2] + 2[(x + 1)^2]cosA
1 = (2[(x + 1)^2])(1 - cosA) = 2[(x + 1)^2][1 - (x/2)]
1 = 2[(x + 1)^2][(2 - x)/2] = (x^2 + 2x + 1)(2 - x)

(I wish I had time to finish this now, but I've got "real life" things that need to be done, and it's been too long since I solved a trinomial. I hope to get back to this tonight.)

Posted by TomM on 2002-06-18 13:52:27