I must be missing something on this question too. I'm usually pretty good with "Aha!" Geometry questions, but I can't see this one.
I've tried interior angles, and can't get anything other than 180=180, or A=A.
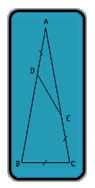
I've tried working out the height of the triangle (2 Cos (a/2) + Cos (3a/2) = 1 / (2 * Tan (a/2))) but can't get to anywhere nice with it.
I've tried setting AD=DE=EC=CB=1 (the value obviously doesn't matter, but 1's nice) and working out lengths based on the center trapesium (formed by D-D'-E-E' where D' and E' are D and E reflected about the vertical axis in the diagram), but I've got that ending up at some horrible quartic, which I refuse to solve (although looks like it'll give the right answer if I could be bothered...)
Please tell me there a nicer way of doing this...
By the way - in case people can't find a better solution, my current quartic seems to have boiled down to:
y^4 - 4*y^3 + 3*y^2 + y - 1 = 0
where the angle BAC is 2*InvSin(0.5/y)
See - lovely, isn't it? :-(
 Given that:
Given that:


