*slaps head*
I'm such an idiot!
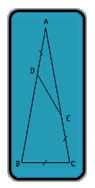
Say the angle we're looking for is "a" and the length BC=CE=ED=DA=1.
Angle AED must also be "a" (as AED is an isoceles triangle), so ADE must be "180-2a". Therefore BDE is "2a". So, line DE must be (3a/2) from the vertical. So, the "vertical" height difference between D and E must be Cos (3a/2)
That's part 1.
Part 2:
Make a trapezium D-D'-E'-E' as mentioned in my last post (where D-D' and E-E' are horizontal lines). Make length AB to 'L'.
We can see D-D' is 1/L and E-E' is 1-1/L.
Therefore EF is (1-1/L)-(1/2*((1-1/L)-(1/L))) = (1-1/L) - (1/2 - 1/L) = 1/2
Also, we know that DE is 1 (given).
So, using Pythag on DEF, we can see that:
(1/2)^2 + (Cos(3a/2))^2 = (1)^2
i.e.
(Cos(3a/2))^2 = 3/4
So, Cos (3a/2) = sqrt (3) / 2
"Sqrt (3) / 2" is a well known Cos value:
3a/2 is 30 degrees
So, at last: a = 20 degrees!
Thank heavens for that!!!
 Given that:
Given that:


