(In reply to
re: Hints ! like answer ! by levik)
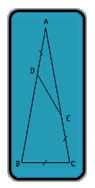
We will prove Triangle DEF = Triangle FEC (we have DE=EC, and common line of both triangle is FE)
Step 1: (only prove angle FEC = angle DEF)
now we have triangle FEC= Triangle FBC because
BC=EC, common line is FC, and angle BCF= angle FCE as CF is a bisectrix of C
so we will have angle FBC=angle FEC.
besides : we have angle A = angle DEA
Angle A + Angle B + angle C = 180 = Angle DEA +Angle DEF +angle FEC
==> angle DEF= Angle B= Angle C=FEC
So now we have triangle DEF= triangle FEC
==>angle FDE= angle FCE=1/2 angle C as CF is a bisectrix of C
also we have FDE=2 angle A
===>B=C=4A==>A=20
|
|
Posted by vohonam
on 2002-06-20 17:07:07 |
 Given that:
Given that:


