(In reply to
re(3): Solution? by levik)
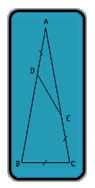
Knowing that Angle BAC = 20°, it is easy to see what each of the other angles must be and which lines must be equal, but it makes it harder to remember whether a particular one was actually proven.
I think that I may have finally reconstructed Vohanam's original proof, or something close to it.
First, call the measure of Angle BAC "A" and the measure of Angles ABC and ACB "B"
A + 2B = 180° [Call this Equation One]
Note also that Angle AED = A, (because triangle ADE is isosceles)
And Angle BDE = 2A (exterior angle)
Also, Angle DEC = 180° - A
But 180° - A = 2B (by Equation One)
So Angle DEC = 2B
Now draw the bisector of Angle BCE, intercepting DB at point F,
And also draw EF
Triangles FCE and FCB are congruent (SAS) because
FC = FC
Angle FCE = Angle FCB = B/2 (Definition of bisector)
CE = CB (given)
So Angle CEF = Angle CBF = B (corresponding angles of congruent triangles)
Angle DEC = Angle DEF + Angle CEF
2B = Angle DEF + B
or Angle DEF = B
Now we get triangles DEF and CEF congruent (SAS) because
EF = EF
Angle DEF = B = Angle CEF
ED = EB (given)
So Angle FDE = Angle FCE (corresponding angles)
But Angle FDE = Angle BDE = 2A
And Angle FCE = B/2
So 2A = B/2
B = 4A
But Equation One says that 180° = A + 2B = A + 2(4A) = 9A
So A = 20°
|
|
Posted by TomM
on 2002-06-21 11:08:36 |
 Given that:
Given that:


