If you drew a dot on the edge of a wheel and traced the path of the dot as the wheel rolled one complete revolution along a line, then the path formed would be called a cycloid (shown below), combining both forward and circular motion.
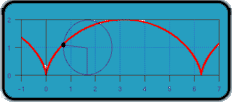
If a wheel of radius 1 traces out such a path, what is the length of the path formed by one complete revolution?
To find the distance the dot travels, integrate the speed of the dot over the time of travel. To find the speed of the dot, find the length of the velocity vector. To find the velocity vector, take the derivative of a function that describes the path of the dot over time. To find that function, well, read on.
The problem doesn't state that the wheel's speed is constant, or what that speed is, but we'll just assume that it is moving at 1 unit per second. It won't affect the answer, and it'll make the math easier. This means that it takes 2π seconds to make a complete revolution.
First, pretend that the wheel is just rotating on a fixed axis, centered at the origin. Assume, as per the diagram, that the dot starts at the bottom of the wheel. A function that describes the motion of the dot in the x direction is -sin
t. In the y direction, the dot follows a path of -cos
t. In actuality, the center of the wheel is 1 unit above the y axis, and also travels in the direction of the x axis at a rate of 1 unit per second. Thus, the position of the dot at every point in time is:
p(
t) = <
t - sin
t, 1 - cos
t>
The velocity of the dot is the derivative of the position, so:
v(
t) = (
d/
dt)
p(
t)
= <(
d/
dt)(
t - sin
t), (
d/
dt)(1 - cos
t)>
= <1 - cos
t, sin
t>
The speed of the dot at any given time is:
s(
t) = |
v(
t)|
= √((1 - cos
t)² + (sin
t)²)
= √(1 - 2cos
t + cos²
t + sin²
t)
= √(2 - 2cos
t)
The final answer is the integral of this function from 0 to 2π. Anybody got a table of integrals handy?




