If you drew a dot on the edge of a wheel and traced the path of the dot as the wheel rolled one complete revolution along a line, then the path formed would be called a cycloid (shown below), combining both forward and circular motion.
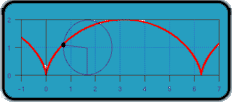
If a wheel of radius 1 traces out such a path, what is the length of the path formed by one complete revolution?
(In reply to
Solution by friedlinguini)
Aha! Half-angle identity to the rescue!
1 - cos t = 2 sin² (t/2)
The formula for the length, then, is Integral(s(t)) evaluated from 0 to 2π.
Integral(s(t)) = Integral(√(2 - 2cos t))
= Integral(√4sin² t/2))
= Integral(|2sin t/2|)
Note that we are only interested in values of t between 0 and 2π. For these values, 2sin t/2 is always positive. This lets us drop the absolute value part
= Integral(2sin t/2)
= -4cos t/2
Evaluating from 0 to 2π gives
-4cos π + 4cos 0 = 8.




