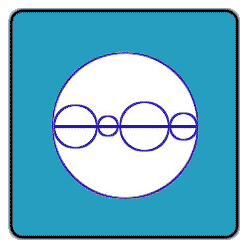
Prove that the sum of the perimeters of the smaller circles in the
Bigger circle is equal to that of the bigger circle. (The centres are on the line given which is the diameter of the bigger circle.)
perimeter = 2*pi*radius
radius = diameter/2
disignate diameter of the large circle to D
designate teh diameters of the small circles from left to right as d1, d2, d3 and d4
The drawing shows D=d1+d2+d3+d2
Therefore D/2= (d1+d2+d3+d4)/2 OR (d1/2) + (d2/2) + (d3/2) + (d4/2)
radius = dimaeter /2
therefore R (radius large circle = r1+r2+r3+r4 (other radii)
THerefore
P (perimeter large) = 2 * pi * R
p1 = 2 * pi * r1
p2 = 2 *pi * r2
p3 = 2 * pi * r3
p4 = 2 * pi * r4
p1+p2+p3+p4 =
(2*pi*r1)+(2*pi*r2)+(2*pi*r3)+(2*pi*r4)=
2 * pi *(r1 + r2 + r3 + r4) =
2 * pi * R =
P =
QED





