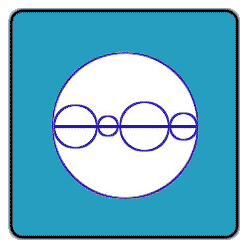
Prove that the sum of the perimeters of the smaller circles in the
Bigger circle is equal to that of the bigger circle. (The centres are on the line given which is the diameter of the bigger circle.)
Well, the nature of the problem lies on selecting the diameter of the circles in the interior of the biggest of them all. The sum of all the diameters of the little circles must be equal to the diameter of the big circle, and the little circles can't intersect un two points with each other, so, in this situation you must select the diameters so that they all sum to give the big diameter. With this, in the sum of perimeters equal to the perimeter of the big circle, Pi is cancelled, so you get D1+D2+D3+D4=D5 or R1+R2+R3+R4=R5, this is the proporcionality of the perimeter to the diameter.
It is a good logical problem.
|
|
Posted by Antonio
on 2003-08-21 16:14:35 |





