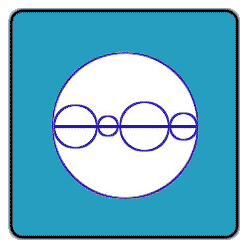
Prove that the sum of the perimeters of the smaller circles in the
Bigger circle is equal to that of the bigger circle. (The centres are on the line given which is the diameter of the bigger circle.)
I posted a comment about proportionality, but the problem seems very easy because you have to choose the diameters of the little circles in order to fill the large diameter. So, 2*Pi*R1+2*Pi*R2+2*Pi*R3+2*Pi*R4=2*Pi*R5 All 2*Pi terms are cancelled and you get R1+R2+R3+R4=R5 the sum of all perimeters are the same as the big perimeter as the sum of all radii are the same as the large radius.
|
|
Posted by Antonio
on 2003-08-22 02:25:28 |





