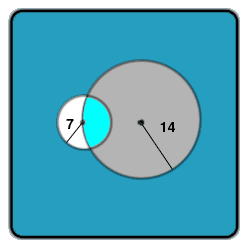
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.
(P.S -The answer might not be elegant)
Since the problem is in the geometry section, it is solved using the proportionality of angle-area. Using trigonometric telations, the general formula would be:
Area = (1/360)*[ R1²*Pi*(180-acos[(2*R2²-R1²)/(2*R2²)]) + 2*R2*(R2*Pi*acos[(2*R2²-R1²)/(2*R2²)]-180*R1*cos((acos[(2*R2²-R1²)/(2*R2²)])/2)) ]. Where 0≤R1≥R2 and R1≤R2≥∞
With R1=7cm and R2=14cm, the common area is: 68.7502555449cm²
No calculus needed.
|
|
Posted by Antonio
on 2003-08-31 07:49:32 |



