Try relating the angle A using the characteristics of an isoceles triangle, where two angles are the same and the other must be 180 minus the two already counted as the same. I managed to solve the problem using intersecting linear ecuations along with a series of angle relations that as I said in the begining, is pure isoceles relation. I put the coordinate origin in the vertex A and the x-axis pointing towards one of the isoceles vertex. I found a distance X that marks the intersection of one side of the isoceles and the line inside the triangle, I amr refering to the intersection in E perpendicular to AB. Such distance X is (I called L to any AD, De, EC, BC) L*tan(2*A)/(Tan(2*A)-Tan(A)). The side AE=X/cos(A)=L*tan(2*A)/(Tan(2*A)-Tan(A))/cos(A). With AE in therms of A and L, we use the law of cosines and get L²=(AE²+L)²+(AE²+L)²-2*(AE²+L)*(AE²+L)*cos(A). Replaceing AE and simplifying this ecuation we finally get 2*(1-cos(A))=(cos(A)/(cos(A)+(tan(2*A)/(tan(2*A)-tan(A)))))². We solve this equation to find A. A=20 degrees
|
|
Posted by Antonio
on 2003-09-04 09:51:01 |
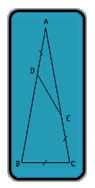 Given that:
Given that:


