Look at this shape:
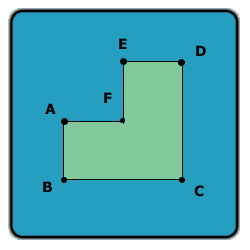
Assume AB = AF = FE = ED and BC = CD, and all the angles in the shape are 90 degrees.
Let A be the area of this shape (in cm^2), and P -- the perimeter of this shape (in cm).
If A - P is 60, what is the length of line AC?
Let x be the length AB, AF, etc.
Then, the perimeter P = 8x, and the area of the figure A = 3x².
A - P = 60
3x² - 8x = 60
3x² - 8x - 60 = 0
(3x + 10)(x - 6) = 0
x = 6, -10.
Obviously, the distance in question must be positive, so x= 60.
Then, AC is the hypotenuse of a right triangle with legs 6 and 12.
Thus, AC² = 6² + 12²
AC = √180
AC = 6√5
AC ~= 13.4164
|
|
Posted by DJ
on 2003-10-10 09:20:37 |



