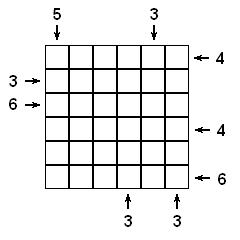
|
Label the columns A-F from L to R, and label the rows 1-6 from top to bottom.
From the 6's shown, the third row must be 123456 while the bottom row is 654321. From the 5 given, the first column from the left must be 231456.
2xxxxx
3xxxxx
123456
4xxxxx
5xxxxx
654321
Building F1 is not a 1 or 2 and is the first of four increasing buildings from R to L, so it must be 3. E1 is either a 1 or 4, but a 1 would cause column E to have either more or less than three visible buildings, so E1 must be 4. E5 must be 6; a 6 elsewhere in column E would violate the number of visible buildings either in column E or row 4. E2 must be 1. 2xxx43
3xxx1x
123456
4xxx3x
5xxx6x
654321
B5 is neither 2 nor 5, therefor the one diagonal with numbers 1-6 must be A1-F6, making B2 4 and D4 5. D5 cannot be 6, and a 6 in D1 would not satisfy 4 visible buildings in row 1, so the 6 in column D is D2. Thus D1 is 1 and D5 is 2.
2xx143
34x61x
123456
4xx53x
5xx26x
654321
B1 cannot be 5, so C1 is 5 and B1 is 6. C2 cannot be 5, so F2 is 5 and C2 is 2. F4 cannot be 4, so F5 is 4 and F4 is 2. B4 cannot be 6, so C4 is 6 and B4 is 1. B5 is 3 and C3 is 1.
265143
342615
123456
416532
531264
654321 |