Cubic Routes (Posted on 2008-11-26)

The image is the net of a cube. Consider the vertices and face centres as forming six separate networks with each having five locations.



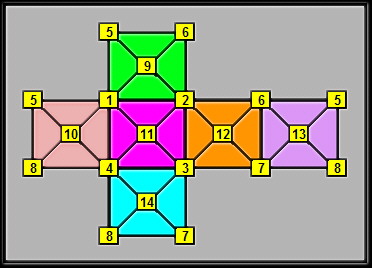
The object is to allocate each of the 14 locations a unique letter of the alphabet such that the letters contained in each of the six networks reads as a five letter word.

The word may begin at any point of the network with successive letters being adjacent to its predecessor. For example, M, I, N, E, D may occupy the respective positions of 1, 2, 3, 4, 11.

Note that the word D E N I M is readable in the reverse direction and thus yields 2 words for that network.

With the latter thought in mind, how many words can you derive from your six networks? [I have 9 and used 4 vowels.]

Note: Please try to limit words to what might be readily accessible in a common "pocket" English dictionary.

	Submitted by brianjn
No Rating
Solution:	(Hide)
This is my offer which will be but one of the possible solutions. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 S C O L T A R E K I D B W V 1 2 6 5 9 S T A C K (T A C K S) 1 5 10 4 8 S T I L E 1 2 3 4 11 S C O L D (C O L D S) 2 3 12 7 6 C O B R A (C A R O B) 13 6 5 8 7 W A T E R 4 3 14 8 7 L O V E R Dej Mar has typically worked on this. Frankly, at the time of writing I'm not sure what was my challenge. As I look at what I offered as the "Official Solution" I'm feeling that my thought was a minimum challenge, so again I acknowledge Dej Mar.

	Subject	Author	Date
	another solution	Dej Mar	2008-12-01 02:02:16
	A solution	Dej Mar	2008-11-27 07:09:55