The network represents a map of the edges and vertices of a
hypercube or more precisely, a tesseract when imposed within 2D space.
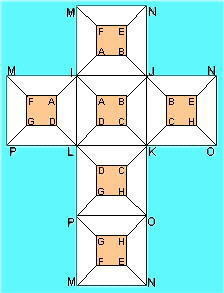 |
The orange squares represent the faces of the internal cell, a cube in 3D space, and is defined by vertices A to H. The larger bolder letters, I to P are the vertices of the outer cell/cube.
The diagonal lines are the edges which link the inner to the outer forming the faces that configure the cells which interface to the inner and outer cells.
Let each hypercell have a value which is the vertex sum of each of its enclosing faces (or three times the sum of its 8 vertices).
|
The vertices are to be numbered uniquely from 1 to 16, and for consistency of reference, let
A always be 1.
Find sets of values for A through P so that all the cells have the same value.
Note: while the on-line calculator may be useful, a spreadsheet should prove more valuable for those able to use one.
|
|
Submitted by brianjn
|
|
Rating: 4.0000 (1 votes)
|
|
|
Solution:
|
(Hide)
|
1,14,8,9,10,13,7,6,4,12,5,15,3,11,2,16
If the Cell table is set up in a spreadsheet as an array of cells, a little similar to that in the problem,
eg:
A | B | C |.....
1 | 2 | 3 |.....
one begins to see patterns emerging in how pairs of data (eg Cell 1 and Cell 2, or the left half of a pair compared with the right half) might be manipulated.
I do note that the number 34 is apparent in the background of calculations, 4 * 34 = 136, 6 * 34 = 204!
I am wondering if the 4 x 4 "magic square" has any significance here".
Originally the position of some C and D labels was incorrect but upon relabeling they were still incorrect.
The graphic now correctly matches the body text.
Daniel's comment @ #3 is different to that above.
As so often happens Charlie gives quite an analysis of a problem. Here is no exception.
The reader might also care to Screen Print Charlie's list, under the computer listing of his first comment and put the values through the javascript "calculator".
|




