(In reply to
Answer by K Sengupta)
By conditions of the problem, we obtain:
A + 2B = 2*pi rad, where A = < BAC and:
< ACB = < ABC = B .......(I)
Also, since Triangle AED is isosceles, it follows that:
< AED = A, while < BDE = < AED + < ADE = 2A
Again, < CED = 2*pi - A = 2B in terms of (i)
We now draw BP which bisects < BCE and meets DB at the point Q. We join PQ.
Thus, triangles QCP and QCB are congruent, and accordingly:
< QPC = < QBC = B
But, < DPC = < DPQ + < CPQ
Or, 2B = < DPQ + B, giving:
< DPQ = B
Thus, it follows that the triangles DPQ and CPQ are congruent, giving:
< QDP = < QCP
But, < QDP = < QCP = 2A, and:
< QCP = = B/2, so that:
2A = B/2
Or, B = 4A
Substituting this into equation (i), we obtain:
9A = 2*pi rad, giving A = 2*pi/9
Consequently, the required measure of the angle A is 2*pi/9 radians.
Edited on August 21, 2007, 11:15 am
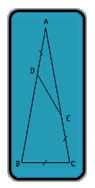 Given that:
Given that:


