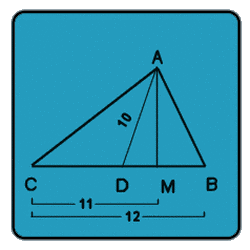
If ABC is a right triangle, the hypotnuse must always be larger then the length of either legs.  SO for ABC:

BC>AC....

But BC=12 and the solution for AC is 14?  This can't be true for a real triangle. 

Another approach to the problem yields a different answer.

Triangles ABC and MAC are similar because:

angle BAC= angle AMC= 90

Angle BCA= Angle ACM

Therefore:  (AC/CM)=(BC/AC) or AC^2=BC*CM

BC=12 and CM =11 so AC^2= 12*11=132

AC=sqrt132 =(approx) 11.5

Now, why don't both answers agree??????