You may find this problem similar.

In a cube of side 4, I pack eight spheres of unit radius.

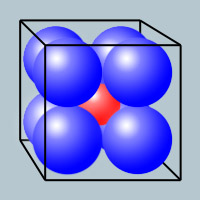
What is the largest sphere I can place in the center (such that it doesn't overlap any of the other spheres)?

firstly draw an imaginary cube using the centres of each of the spheres as the points on the box.
then use Pythagarus (i think) theory across one face to find the length of the diagonal. use this length as the base in a second triangle and use the measure of one edge as the second, calculate the third using said theory. subtract the length of to radii from this and the diameter of the sphere in the middle is given, half this to show radius

1. (R1+R2)^2+(R3+R4)^2=X^2
X=Diagonal length across centre of spheres on same face
2 (R5+R6)^2+X^2=Z^2
Z=length across centre of spheres directly opposite
3. (Z - (R1+R2))/2 = Radius of small sphere

placing in the figures

1. (1+1)^2+(1+1)^2=X^2
1a. Sqroot of X=2.8284271247
2. (1+1)^2+X^2 =Z^2
2a. Sqroot of Z=3.4641016151
3. (3.4641016151-(1+1))/2=0.732050807568 units of length for the radius of the centre sphere.

I have a feeling that there is an easier way to calculate this, but without an education i'm unable, i should have tried harder in school.

Phil
Edited on February 9, 2004, 7:11 am

Posted by Phil on 2004-02-09 07:03:53