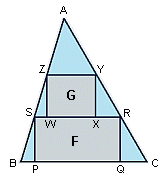
ABC is an acute-angled triangle with area 1. A rectangle F(PQRS) has its vertices on the sides of the triangle, with P and Q on BC, R on AC, and S on AB. Another rectangle, G(WXYZ), has its vertices on the sides of triangle ASR, with W and X on RS, Y on AS, and Z on AR.
What is the maximum total area of F and G?
Through S draw a parallel to AC; let T be its intersection with BC. Through Z draw another parallel to AC; let V be its intersection with RS.
F equals the area of TCRS, and G equals the area of VRYZ. BST and SZV are similar to BAC. Maximizing F+G equals minimizing the sum of the areas of BST, SZV, and ZAY.
Let's call BC=2L so the height of ABC is 1/L. If BT=2H, then the area of BST is H^2/L^2. If SV=2K, then the area of SZV=K^2/L^2. Finally, ZY=2L-2H-2K, so the area of ZAY=(L-H-K)^2/L^2.
Maximizing F+G equals minimizing (H^2+K^2+(L-H-K)^2)/L^2. Differentiating with regard to H and K and equating to zero, shows that this is minimum if H=K=L/3, and in that case, F+G equals 2/3 of the total area.
PS. In the first draft of this text, I had written "parallel to BC", which made no sense, instead of "parallel to AC".
Edited on March 2, 2004, 2:45 pm



