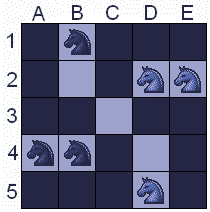
The diagram shows a restricted chess board with three black knights and three white knights. Your goal is to move the pieces so that the same squares are occupied but the colors are reversed. Your first move must use a black piece.

Pieces may move only as a normal chess knight, from one corner of a 2×3 rectangle to the opposite corner. No more than one piece may occupy a single square at a time. No piece may move onto a darkened square. No other rules of chess apply.

One turn is a sequence of moves made by a single piece. Find a solution with the minimum number of turns.

In the other puzzle you have three knights of each color on opposite sides of a 3x3 grid and have to move them to opposite sides.  There is a quick algorithm to solving that puzzle based on an 8-sided star.

I think the solution to this puzzle is similar.  There are three points which are crucial to this puzzle:
- The squares at the corners of the central 3x3 grid can only move to one other square each, namely the ends of the pinwheels counter-clockwise to the square they are in.  Likewise, the only way to get to those squares is from those pinwheel ends (obviously).
- The center square can move to any of the *four* pinwheel ends.
- Teh pinwheel ends are the only squares which can move to either the center square or the corners of the central 3x3 checker board.

There are only two black knights which can move on the first turn (B1, A4).  If you move A4 to the center, then you create a position where no further moves can be made (except moving that knight back to A4).

Posted by Erik O. on 2004-12-10 21:09:17