 How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
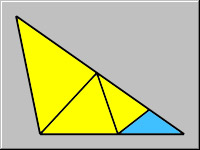
The graphic shows how this obtuse triangle can be divided into almost all acute triangles except one - the blue one. What approach should be used when one must cut an obtuse triangle into acute triangles only?
(In reply to
re: Answer in seven by Thalamus)
I think I can answer part of that. If you don't draw at least one line starting from the vertex with the obtuse angle, you won't solve the problem, so you have to draw at least one line.
I haven't worked out what happens if you draw two or more lines, but if you draw just one line, and it reaches the opposite side, you will either get two right angles (we need acute angles, so that's no good) or an acute angle and an obtuse angle (and we're worse off than when we started)... so the line would stop in the middle.
Of course, you'd have to draw some more lines from that endpoint, and if you draw one, two, or three, you'll get at least a right angle -- or worse, so it's logical that you'd need at least four more lines...
and that's as far as I get tonight!! ;-)
 How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?



