How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse. If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?

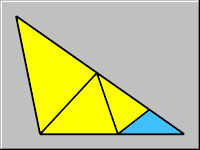
The graphic shows how this obtuse triangle can be divided into almost all acute triangles except one - the blue one. What approach should be used when one must cut an obtuse triangle into acute triangles only?