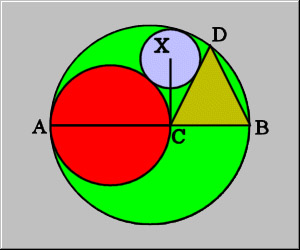
Consider a circle O with a diameter AB, shown here in green. Draw a second circle (red) with diameter AC, such that C is on AB. Draw an isosceles triangle with base CB and third vertex D on circle O. Draw a third circle (X), tangent to the first three figures. Prove that the line from C to the center of circle X is perpendicular to AB.

Let the diameters of circles AC and AB be 2a and 2b respectively. Let M be the midpoint of line segment CB. If we let C be the origin (0,0), then we have A = (-2a,0), B = (2b-2a,0), and M = (b-a,0). Circle AB has the equation

   (x+2a-b)^2 + y^2 = b^2.

Plugging the x-coordinate of D ( =b-a ) into this we get

   D = (b-a,sqrt(b^2-a^2)).

If circle X has radius r, then its center X = (x,y) must be one of the intersections of the circles:

   (x+a)^2 + y^2 = (a+r)^2  and  (x+2a-b)^2 + y^2 = (b-r)^2.

Solving for r we get

   r = (b-a)(2a+x)/((a+b).

Since we want the center to be on the y-axis ( x=0 ),

   r = 2a(b-a)/(a+b).

Solving for y gives

   y = 2a*sqrt(2b(b-a))/(a+b).

Now we must show that circle X is tangent to line CD.

Let T be a point on circle X such that CT is tangent to circle X and T is on the same side of line CX as point D. Clearly circle X is tangent to line CD if triangles CXT and DCM are similar.

Both are right triangles with

   CM = b-a  and  DM = sqrt(b^2-a^2)

   XT = 2a(b-a)/(a+b)  and  XC = 2a*sqrt(2b(b-a))/(a+b).

With these four values, I will let you verify that the triangles are similar.

Posted by Bractals on 2004-09-10 16:18:51