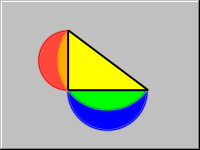
Given a right triangle, draw the three following semicircles:
- The semicircle with diameter formed by one of the legs and extending away from the triangle.
- The semicircle with diameter formed by the other leg and extending away from the triangle.
- The semicircle with diameter formed by the hypotenuse and extending towards the triangle.
Prove that the area of the two crescents (shown in RED and BLUE) formed by the three semicircles equals the area of the triangle.
The basis for this, of course, is Pythagorean. The Pythagorean theorem will work with any consistent shape, e.g., triangles, squares, circles, semicircles, pentagons. To make it work with semicircles, multiply both sides of c²=b²+a² by pi / 8 to get pi(c²)/8 = pi(b²+a²)/8. This shows the sum of the two smaller semicircles to equal the larger semicircle.
Now, think of the cute coloured sketch above. The larger semicircle is folded back over the triangle, essentially subtracting the triangle, leaving the tiny crescents which are over the smaller semicircles and are essentially subtracted from them, leaving the two larger crescents whose sum obviously must be equal to the triangle.
Try this with squares and you'll get similar results. What the Ancients didn't realise immediately was that the non-transcendental results with the circles occurred simply because pi had been subtracted out.
Now, isn't this proof absolutely so better? Hugs. -CeeAnne-
|
|
Posted by CeeAnne
on 2004-10-11 16:35:37 |
 Given a right triangle, draw the three following semicircles:
Given a right triangle, draw the three following semicircles:


