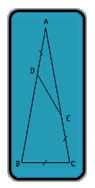
May I humbly submit yet another solution?
Let a be the angle BAC and let d be the length of AB. Flip the path ADEC about the perpendicular bisector of AC to get the path CFGA (G is on AC, of course). Now flip the path CFGA about the perpendicular bisector of BC to get the path BF'DA (G flips to D because both are at distance d from A). We show that F=F'.
The quadrilateral DAGF is a parallelogram because angles DAG and FGA are supplementary (angle FGC equals a). Hence the length of DF is d. Similarly, the length of GF' is d. The intersection X of the lines DF and GF' must be at distance d from both D and G (because ADXG is also a parallelogram), so that intersection must be X=F=F'. But then BF, FC, and BC all have length d (all segments of the flipped paths have length d), and so triangle BFC is equilateral. Therefore its angles must each equal [(180-a)/2]-a (angle ABC minus a), or 90-3a/2. Thus this angle is 60 degrees. Hence
60=90-3a/2, or
3a/2=30, or
a=20.
|
|
Posted by McWorter
on 2005-03-06 04:22:23 |
 Given that:
Given that:


