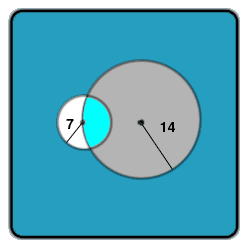
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.
(P.S -The answer might not be elegant)
I proposed an earlier solution which fortunately disappeared into cyberspace. I inadvertently submitted the area of the 7 cm circle!
Firstly I offer the approximate value of 67 sq cm.
To provide some brevity I have detailed some construction, defined the formula used and from there allowed some license in providing values for different sections of the problem.
So, Construct:
1. A line to join the centres (a line of symmetry)
2. A chord (common) to join the circumference intersections.
3. A quadrilateral using the two centres and circum. intersects as vertices.
This provides two overlapping sectors whose combined segments form the are in question.
AREA OF SEGMENT is given by:
[PI*r*r*(radial angle of sector)/360 - chord length*(Radius - Segment height)/2]
RADIAL ANGLE can be established using the Cosine Theorem; ie, a*a = b*b + c*c -2bcCosA
or CosA = [(radius*radius)*2 - (chord)*(chord)]/92*radius*radius)
CHORD LENGTH (x) = 2* height of a 14,14,7 cm triangle.
SEGMENT HEIGHTS are:
1. length (y) of shorter section of symmetrical line at intersection with chord
2. 7 cm radius diminished by 'y'
CHORD LENGTH AND SEGMENT HEIGHTS require a pair of simultaneous equations based on a 14,14,7 triangle.
These are:
1. x*x = 7*7 - y*y
2. x*x = 14*14 -(14-y)(14-y)
which resolve to:
y = 49/28 or 1.75 cm
and x = 6.78 cm (approx)
so that the Chord length is 13.56 cm (approx)
The Radial angle in the large circle = 56.72 Degrees
and that of the smaller is 151.045 Degrees.
The relevant segments therefore are: 13.99 sq cm and 52.73 sq cm, totalling 66.72 sq cm.
I applied a 'confirmation' test to my result.
I considered the proportions of the area of the 7 cm sector and the area of the 7 cm segment in relation to the 7 cm circle area. Respectively they equate to .042 and 0.34.
Seems fair to me.



