The graphic represents the partially exploded net of a stellated cube as viewed in its cubic layout; each face is a right pyramid viewed from above.

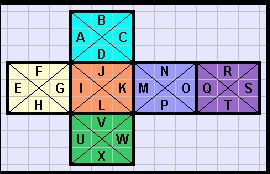
As with a problem of similar concept the letters are placeholders for numerals; in this case they are 1 through 24, [A=1].

The apices of the pyramids form 'external' vertices
while those which describe the foundation cube are the 'interior' vertices.

1. What is the global sum of the 6 'external' vertices and then their average?
2. What is the global sum of the 8 'interior' vertices and then their average?
3. How can the faces be labeled to optimise both #1 and #2 simultaneously?

The optimum outcome would be for all vertices to have the value of their type, 'external' and 'internal'.

Completely by trial and error with a process.  I numbered the faces A-X with 1 through 24, and entered the information into excel.  I then swapped the values of the faces with similar values ("1" with "2") and if the average standard deviation for the entire polyhedron was reduced, I kept the swap.  If not, I returned the values to their previous position. I then moved on to swap "2" and "3", then "3" and "4" etc.  This was done multiple times.  I reached a dead end after 15 or so rounds of swapping.

My answer:
External Vertices: 
Average = 50  Deviation = 0.33  Max deviation = 1

Internal Vertices:
Average = 75  Deviation = 0.25  Max deviation = 1

A 24
B 9
C 15
D 2
E 17
F 6
G 20
H 7
I 14
J 8
K 18
L 10
M 13
N 19
O 5
P 12
Q 11
R 16
S 3
T 21
U 23
V 1
W 22
X 4

Vertices/Sum/Deviation/Deviation Squared

ABCD 50 0 0
EFGH 50 0 0
IJKL 50 0 0
MNOP 49 1 1
QRST 51 1 1
UVWX 50 0 0

ABEFRS 75 0 0
ADFGIJ 74 1 1
BCNOQR 75 0 0
CDJKMN 75 0 0
GHILUV 75 0 0
EHSTUX 75 0 0
KLMPVW 76 1 1
OPQTWX 75 0 0

Posted by Leming on 2007-06-29 10:43:35