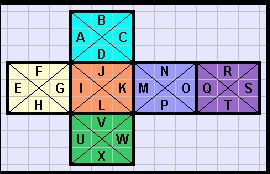
As with a problem of similar concept the letters are placeholders for numerals; in this case they are 1 through 24, [A=1].
The apices of the pyramids form 'external' vertices
while those which describe the foundation cube are the 'interior' vertices.
1. What is the global sum of the 6 'external' vertices and then their average?
2. What is the global sum of the 8 'interior' vertices and then their average?
3. How can the faces be labeled to optimise both #1 and #2 simultaneously?
The optimum outcome would be for all vertices to have the value of their type, 'external' and 'internal'.



