The graphic represents the partially exploded net of a stellated cube as viewed in its cubic layout; each face is a right pyramid viewed from above.

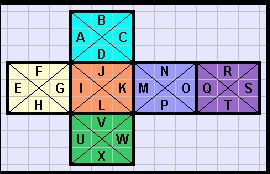
As with a problem of similar concept the letters are placeholders for numerals; in this case they are 1 through 24, [A=1].

The apices of the pyramids form 'external' vertices
while those which describe the foundation cube are the 'interior' vertices.

1. What is the global sum of the 6 'external' vertices and then their average?
2. What is the global sum of the 8 'interior' vertices and then their average?
3. How can the faces be labeled to optimise both #1 and #2 simultaneously?

The optimum outcome would be for all vertices to have the value of their type, 'external' and 'internal'.

1. Each lettered face contributes to only one external vertex, so the global sum of the external vertices is just the total of all the numbers from 1 through 24, or 25*12=300. Since there are 6 of these vertices, the average vertex has a total of 50. Alternatively for the average, the average lettered face is 12.5, and each external vertex has four contributors, for an average total of 50.

2. Each lettered face contributes to two internal vertices, so the global sum is 600. There are 8 internal vertices, so the average internal vertex totals 75. Alternatively, there are six contributors to each internal vertex, so the average is 6*12.5=75.

3. In the case of (1), just pair opposite sides of each pyramid so they add up to 25, such as I and K or N and P. There are 12 such pairs, from 1,24 to 12,13.

The case of (2) is more complicated.  I'll have to think more on it.

Posted by Charlie on 2007-06-22 10:09:27