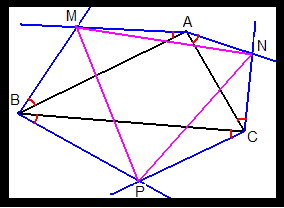
Let ABC be any triangle you draw.

From each vertex, draw two lines outside the triangle, each one at 30' (red arcs) with the sides that meet each other in the vertex.

These 6 lines cross, two by two, at 3 points, named M, N, and P.

Prove that, no matter what triangle ABC you draw initially, the triangle MNP is always equilateral.

(In reply to Napoleon's Theorem by Brian Smith)

Nice, Brian, but I still donīt have a geometric proof, which is my intention when I submitted this problem, presented to me in my times of high-school, and that I never solved.

Edited on October 19, 2008, 10:10 am

Posted by pcbouhid on 2008-10-19 08:30:11