(In reply to
A new theory by TomM)
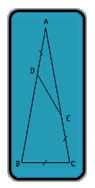
I think that using only the rules about complementary(?) angles, and the sum of interior angles we can solve this problem.
Angle A is what we are trying to find. Let's say it's a degrees. AED will also be a degrees.
Angles B and C are equal, let's say they're b degrees each.
Angle ADE is (180 - 2b) degrees, and angle BDE, its complementary is (2b) degrees.
Since the angles of a quadrangle add up to 360 (you can prove this by dividing it into two triangles), the angle DEC is (360 - 2a - 2b) degrees. (This can be simplified to (180 - a) by plugging in the fact that (a + 2b) = 180, but this last value could have just as easily been derived from the fact that DEC is complementary with DEA, whose value is (a).
Anyone wishes to continue?
|
|
Posted by levik
on 2002-06-18 18:12:42 |
 Given that:
Given that:


