Always equilateral (Posted on 2008-10-14)

Let ABC be any triangle you draw.

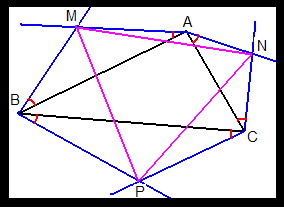
From each vertex, draw two lines outside the triangle, each one at 30' (red arcs) with the sides that meet each other in the vertex.

These 6 lines cross, two by two, at 3 points, named M, N, and P.

Prove that, no matter what triangle ABC you draw initially, the triangle MNP is always equilateral.

	Submitted by pcbouhid
Rating: 4.0000 (1 votes)
Solution:	(Hide)
See two different solutions in the comments. I have another one, using analytic geometry, too long to post here. Unfortunatelly, no pure geometric proof was found... yet.

	Subject	Author	Date
	re(2): Napoleon's Theorem - trig proof	Brian Smith	2008-10-21 03:07:30
	re: Napoleon's Theorem	pcbouhid	2008-10-19 08:30:11
	Napoleon's Theorem	Brian Smith	2008-10-18 23:07:46
	re: Solution	pcbouhid	2008-10-18 12:23:33
	Solution	Bractals	2008-10-14 15:52:10