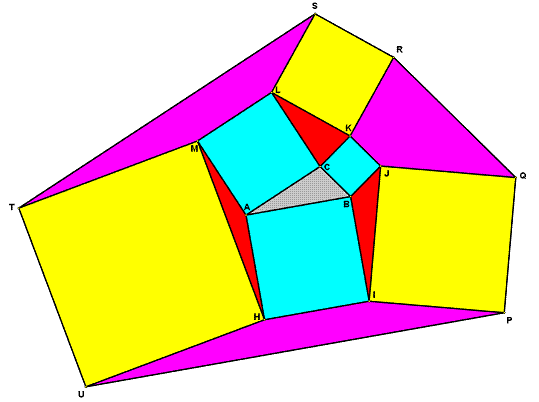
Let a = |BC|, b = |CA|, c = |AB|, d = |KL|, e = |MH|, and f = |IJ|.
Let [WX...Z] denote the area of polygon WX...Z.
PART 1
Using the law of cosines:
a2 = b2 + c2 - 2bc cos(/BAC)
b2 = c2 + a2 - 2ca cos(/CBA)
c2 = a2 + b2 - 2ab cos(/ACB)
d2 = a2 + b2 - 2ab cos(/KCL)
= a2 + b2 - 2ab cos(180-/ACB)
= a2 + b2 + 2ab cos(/ACB)
e2 = b2 + c2 - 2bc cos(/MAH)
= b2 + c2 - 2bc cos(180-/BAC)
= b2 + c2 + 2bc cos(/BAC)
f2 = c2 + a2 - 2ca cos(/IBJ)
= c2 + a2 - 2ca cos(180-/CBA)
= c2 + a2 + 2ca cos(/CBA)
Adding these six equations:
d2 + e2 + f2 = 3(a2 + b2 + c2)
The yellow area is three times the cyan area.
PART 2
We will show that the area of quadrilateral STML
is five times the area of triangle HMA. A similar
argument can be used to show that the area of
quadrilateral UPIH is five times the area of triangle
JIB and the area of quadrilateral QRKJ is five times
the area of triangle LKC.
To do this, we will use complex numbers to show
that ST is parallel to ML and |ST| = 4|ML|. Let the
letters of the figure represent complex numbers
and note that multiplying a complex number by i
rotates that complex number CCW by 90 degrees.
L = C - i(A-C) = C - iA + iC
K = C + i(B-C) = C + iB - iC
S = L + i(K-L) = L + iK - iL
= (C - iA + iC) + i(C + iB - iC) - i(C - iA + iC)
= C - iA + iC + iC - B + C - iC - A + C
= -A - B + 3C - iA + iC
M = A + i(C-A) = A + iC - iA
H = A - i(B-A) = A - iB + iA
T = M - i(H-M) = M - iH + iM
= (A + iC - iA) - i(A - iB + iA) + i(A + iC - iA)
= A + iC - iA - iA - B + A + iA - C + A
= 3A - B - C - iA + iC
S - T = 4(C - A) = 4(L - M)
Let Y be the midpoint of ST, X the midpoint of SY,
and Z the midpoint of YT. Clearly the line segments
LX, LY, MY, and MZ divide STML into five triangles
having the same area.
All that is left is to show that triangle HMA is
congruent to one of these five triangles.
Extend line segment LM to N.
|MT| = |HM| = e
/MTZ = /TMN = 90 - /NMH = /HMA
|TZ| = |MA| = b
Therefore, triangles MTZ and HMA are congruent
by side-angle-side.
The magenta area is five times the red area.
NOTE
Each red triangle has the same area as triangle ABC,
[ABC] = bc/2 sin(/BAC) = bc/2 sin(180-/MAH)
= bc/2 sin(/MAH) = [HMA]
[ABC] = ca/2 sin(/CBA) = ca/2 sin(180-/IBJ)
= ca/2 sin(/IBJ) = [JIB]
[ABC] = ab/2 sin(/KCL) = ab/2 sin(180-/KCL]
= ab/2 sin(/KCL) = [LKC]
Therefore, each magenta quadrilateral has an area
five times the area of triangle ABC.
|