If you drew a dot on the edge of a wheel and traced the path of the dot as the wheel rolled one complete revolution along a line, then the path formed would be called a cycloid (shown below), combining both forward and circular motion.
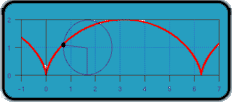
If a wheel of radius 1 traces out such a path, what is the length of the path formed by one complete revolution?



