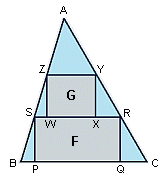
ABC is an acute-angled triangle with area 1. A rectangle F(PQRS) has its vertices on the sides of the triangle, with P and Q on BC, R on AC, and S on AB. Another rectangle, G(WXYZ), has its vertices on the sides of triangle ASR, with W and X on RS, Y on AS, and Z on AR.

What is the maximum total area of F and G?

(In reply to re(3): We are not square (in my original post, they are) by DJ)

OK, let's start afresh, the only reason i said squares was because the dimensions of the theoretical triangle i used were such that the outcome of the shapes F & G were both squares, maybe this is unfortunate,

So to re-iterate the area of F should be equal to ½Height x ½Base, while the area of G should be ¼Height x ¼Base, giving us areas of F=50% total area and G=12.5% total area. F+G=62.5%

I have since recalculated with the DJ's recommendations and have got better results (66.66%) thanks for that

I also realise where i went wrong, i was trying to get the largest area possible with the first rectangle and then doing the same with the second, this is clearly wrong as the calculations show that if the rectangular heights are the same then the smaller rectangle will more than make up for the shortfall in the first.

I guess this long drawn out explanation as actually been an apology of sorts, i shall refrain posting any more comments on maths related issues until i am more sure of what is being asked

Sorry,

Phil (Juggler)

Posted by Juggler on 2004-03-03 19:20:57