Six chess knights are placed on a 4x3 chessboard, three along the top row and three along the bottom, which are labeled as P, Q, R, X, Y, Z, as shown in the figure below.

Exchange the positions of P and X, Q and Y and, R and Z, in minimum possible number of moves.

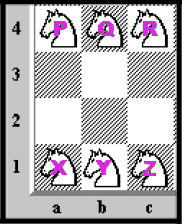
I found a repeating loop in my first and now find a shorter path of 40 moves, but may still have flaws. I'll list the capital letters and chart coordinates as given.

Z-a3, Z-c2, Y-a2, Z-b4, y-c3, Z-a2, R-b3, Z-c1, P-c2, R-A1, P-b4,

R-c2, R-a3, R-c4, Q-a3, P-a2, Q-c2, Q-b4,Y-b1, X-b2, P-c3, P-a4,

P-c3, P-a2, X-a4, X-b2, P-c3, P-a4, R-a3, X-c4, R-c2, X-a3, Q-a2,

R-b4, X-c2, X-a1, R-c2, Q-b4, R-a3, R-c4.   XYZ PQR QED?!

Probably still repeating paths in this line also.   

 

 

Posted by ed bottemiller on 2010-04-05 19:46:17