|
2/3
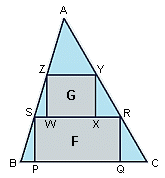
Let k = AR/AC. Triangle ASR is similar to ABC, with all dimensions smaller by a factor of k. Thus, its area is k².
Similarly, triangles BPS and CQR together have area (1-k)². Thus, the area of the bottom rectangle is 1 - k² - (1-k)² = 2k(1-k). Defining h = AZ/AS in a similar way, the area of the top rectangle is 2h(1-h) times the area of the triangle ASR, or 2h(1-h)k².
Notice, now, that the area of F depends only on k, while the area of G depends on both k and h. So, the area of the top rectangle is maximized by taking h=1/2, giving G an area of 2(1/2)(1-1/2)k² = k²/2.
From this, the sum of the areas of F and G is k²/2 + 2k(1-k) = 2/3 - 3/2(k-2/3)². It is simple enough to see that this is maximized when k = 2/3, leaving the joint area of F and G to be 2/3.
It is interesting to note that this value (2/3) is the same regardless of the specific triangle. |